I needed to find the profile of an air conditioning duct that goes through a wall at a 45 degree angle to create a trim piece. Intuitively this will become an ellipse so the equation of an ellipse will be my starting point.
![]()
The question then is what are the semi-major axis a, and semi-minor axis b. The semi-minor axis will remain constant because there will be no stretching in the vertical direction. The semi-minor constant will remain equal to the radius of the original pipe.
Thinking of the semi-major axis I know that as the angle increases towards 90 degrees, the semi-major axis approaches infinity. Below I’ve drawn a slice of the pipe viewed from above with a depiction of what happens when the cross section is rotated by some amount (simulating the profile through the wall at an angle).
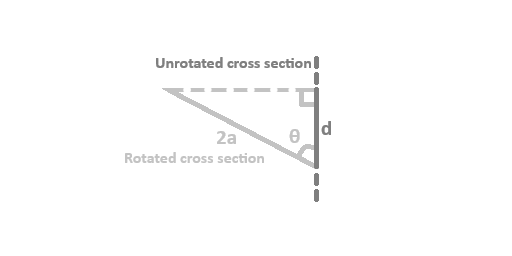
In the figure, d is the diameter of the pipe, and theta is the angle which the pipe is rotated with respect to the wall. As seen in the figure the hypotenuse of the right triangle is actually twice the semi-major axis of the rotated profile.![]()
![]()
Plugging back into the equation of an ellipse:![]()
As theta approaches 90 degrees, cos(theta) approaches 0 resulting in the semi-major axis approaching infinity. I used the 12 1/4″ pipe diameter I needed, plotted the result and sent it to be used for a metal trim piece around the outside of the pipe. It turned out pretty good.